Confidence Intervals
Linear and Generalized Linear Models
Confidence Intervals
Confidence Intervals
CI: Mean
CI: Variance
CI: Regression Coefficients
Hypothesis Testing
Confidence Intervals
- A confidence interval gives a range of plausible values that captures population parameter.
- It reflects uncertainty in point estimates from sample data.
CI: Formula
\[ PE \pm CV \times SE \]
- \(PE\): Point estimate (\(\hat \beta\))
- \(CV\): Critical Value \(P(X > CV) + P(X < -CV) = \alpha\)
- \(SE\): Standard Error of \(\hat \beta\)
\[ (LB = PE - CV \times SE, UB = PE + CV \times SE) \]
Critical Value
A critical value is a cutoff point on a probability distribution used to:
- Construct confidence intervals
- Make decisions in hypothesis testing
It corresponds to a chosen significance or confidence level.
Distributions Used for Critical Values
- Z-distribution (standard normal)
- Used when population σ is known or n is large.
- t-distribution
- Used when population σ is unknown (most common).
- χ² distribution
- For variance tests and CI for σ².
Obtaining Critical Values
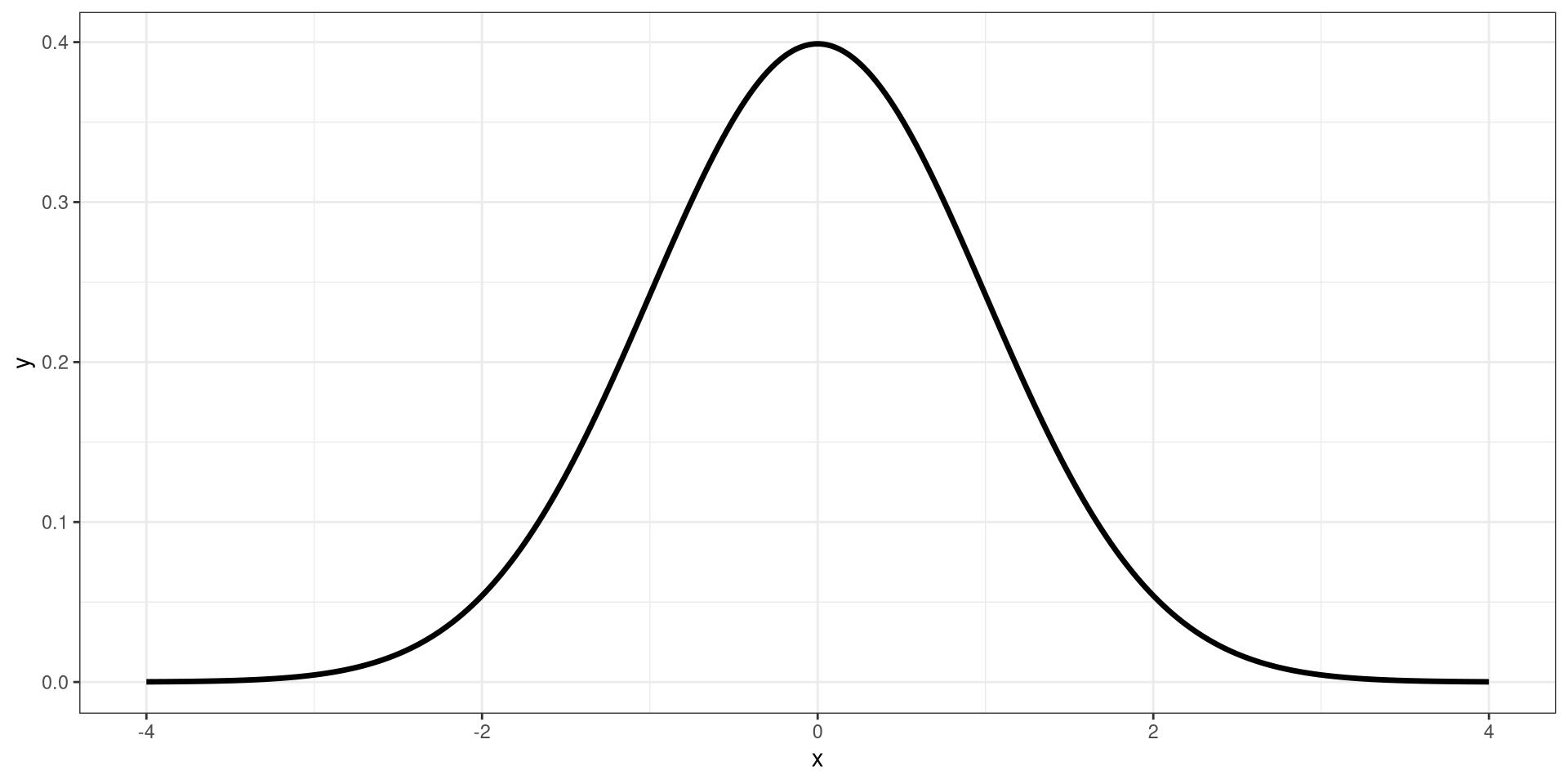
Obtaining Critical Values
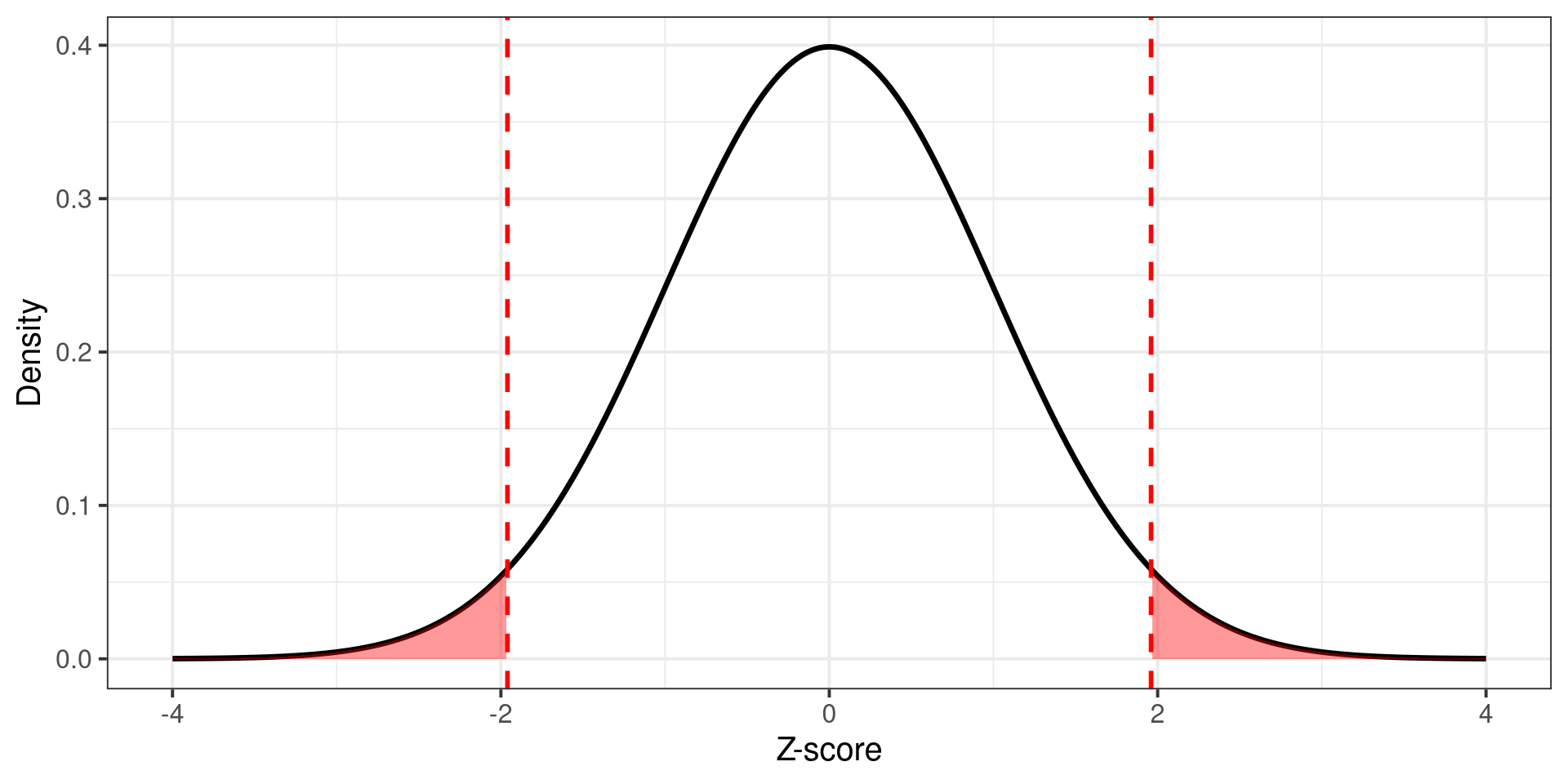
Critical Value Notation
For a confidence level \(1 - \alpha\):
- Z-critical value: \(z_{\alpha/2}\)
- t-critical value: \(t_{\alpha/2, df}\)
Interpretation:
- \(\alpha\) = total probability in both tails
- \(\alpha/2\) = probability in one tail
Interpretation
“We are 95% confident that the true mean lies between A and B.”
- This does not mean there’s a 95% chance the mean is in that interval.
- It means: if we repeated the sampling process many times, 95% of the intervals would contain the true value.
CI Plot
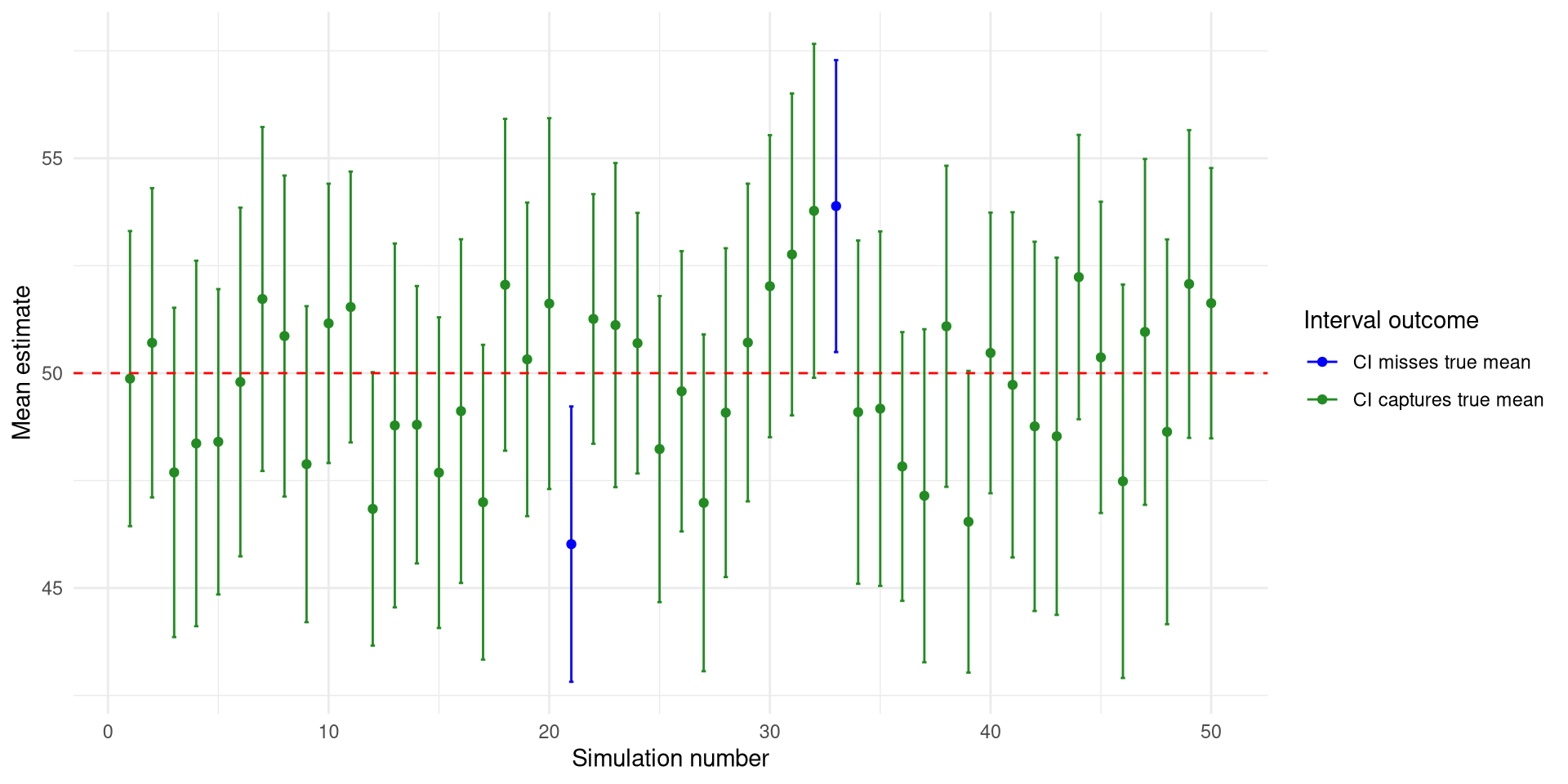
Factors Affecting CI Width
- Sample size (\(n\)): larger \(n\) → narrower CI
- Standard deviation (\(s\) or \(\sigma\)): more variability → wider CI
- Confidence level: higher confidence → wider CI
CI: Mean
Confidence Intervals
CI: Mean
CI: Variance
CI: Regression Coefficients
Hypothesis Testing
CI: Mean
- For a mean, it represents uncertainty due to sampling.
- A 95% CI means: If we repeated sampling many times, 95% of those intervals would contain the true mean.
CI: Formula
A (1 – α) confidence interval is:
\[ \bar{x} \pm Z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} \]
CI: Formula
\[ \bar{x} \pm t_{\alpha/2; df} \cdot \frac{s}{\sqrt{n}} \]
CI: Variance
Confidence Intervals
CI: Mean
CI: Variance
CI: Regression Coefficients
Hypothesis Testing
CI: Variance
We want a confidence interval for the population variance \(\sigma^2\).
Distribution
\[ \frac{(n-1)s^2}{\sigma^2} \sim \chi^2_{(n-1)} \]
This allows us to form a confidence interval for \(\sigma^2\) (variance) and then take the square root for \(\sigma\).
Formula
A (1–α) confidence interval is:
\[ \left( \frac{(n-1)s^2}{\chi^2_{\,\alpha/2,\;df}},\ \frac{(n-1)s^2}{\chi^2_{\,1-\alpha/2,\;df}} \right) \]
CI: Regression Coefficients
Confidence Intervals
CI: Mean
CI: Variance
CI: Regression Coefficients
Hypothesis Testing
Sampling Distributions of \(\hat \beta_j\)
\(\phi\) known
\[ \frac{\hat\beta_j - \beta_j}{\mathrm{se}(\hat\beta_j)} \sim N(0,1) \]
\(\phi\) unknown
\[ \frac{\hat\beta_j-\beta_j}{\mathrm{se}(\hat\beta_j)} \sim t_{n-p} \]
CI: \(\beta_j\)
\[ \hat \beta_j \pm CV \times SE \]
Hypothesis Testing
Confidence Intervals
CI: Mean
CI: Variance
CI: Regression Coefficients
Hypothesis Testing
Hypothesis Testing: Confidence Interval Approach
The confidence interval approach can evaluate a hypothesis test where the alternative hypothesis is \(\beta\ne\beta^*\). The confidence interval approach will result in a lower and upper bound denoted as: \((LB, UB)\).
Decision Making
If \(\beta^*\) is in \((LB, UB)\), then you fail to reject \(H_0\). If \(\beta^*\) is not in \((LB,UB)\), then you reject \(H_0\).